k-means算法详解
前言
俗话说:“物以类聚,人以群分”,在自然科学和社会科学中,存在着大量的分类问题。所谓类,通俗地说,就是指相似元素的集合。
而对于分类问题,我们通常不会提供x与y这样的映射关系,对于这种用机器自动找出其中规律并进行分类的问题,我们称为聚类。
聚类在实际的应用中亦是非常广泛的,如:市场细分(Market segmentation)、社交圈分析(social network analysis)、集群计算(organize computing clusters)、天体数据分析(astronomical data analysis)
K均值(K-means)
在聚类分析中,我们希望能有一种算法能够自动的将相同元素分为紧密关系的子集或簇,K均值算法(K-means)为最广泛的一种算法。k-means是硬分类,一个点只能分到一个类。
接下来我们会以图解的形式讲解该算法。
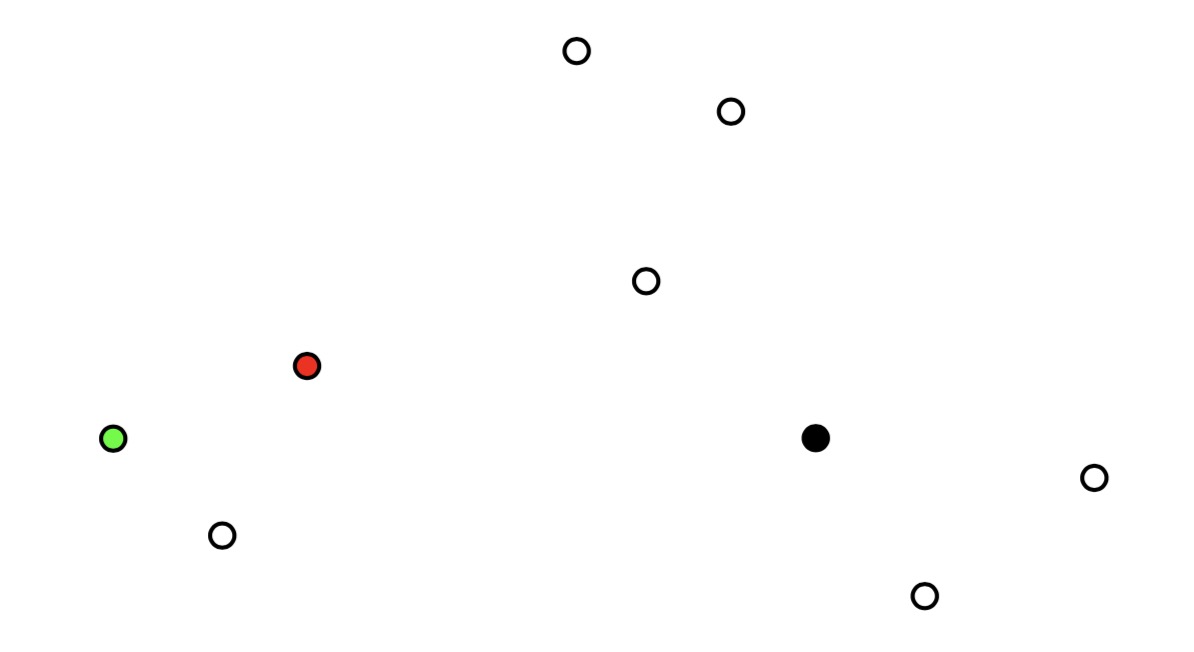
假设我们有9个点,我们要把九个点分为三类
首先,我们在图中随机选择三个点
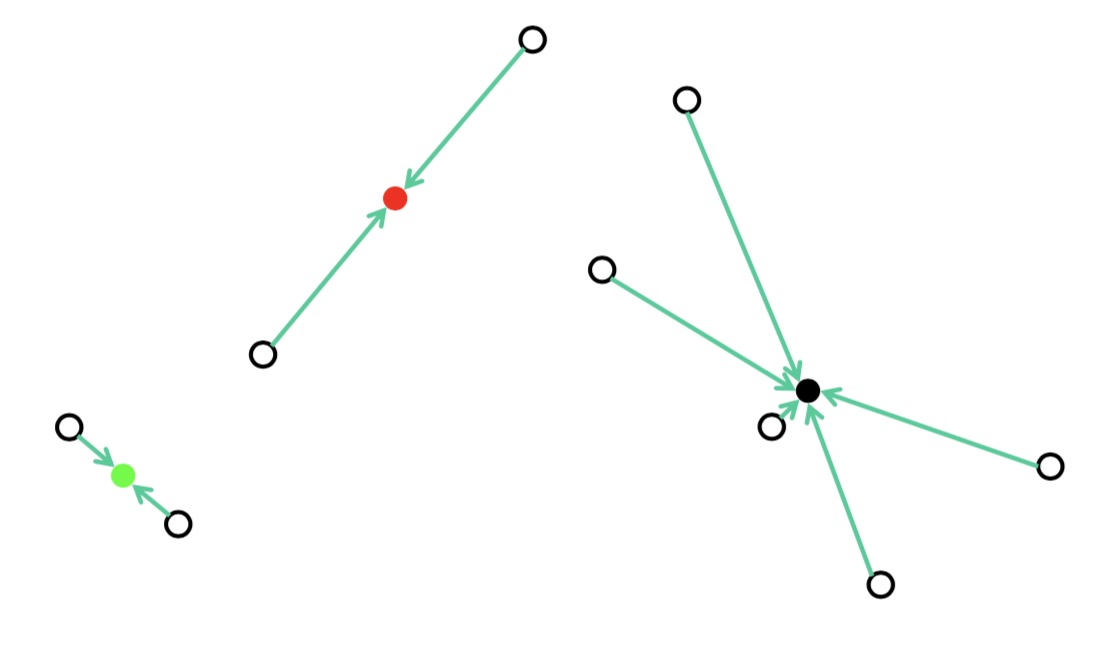
把距离这三个点最近的其他点归为一类

取当前类的所有点的均值,作为中心点
更新距离中心点最近的点
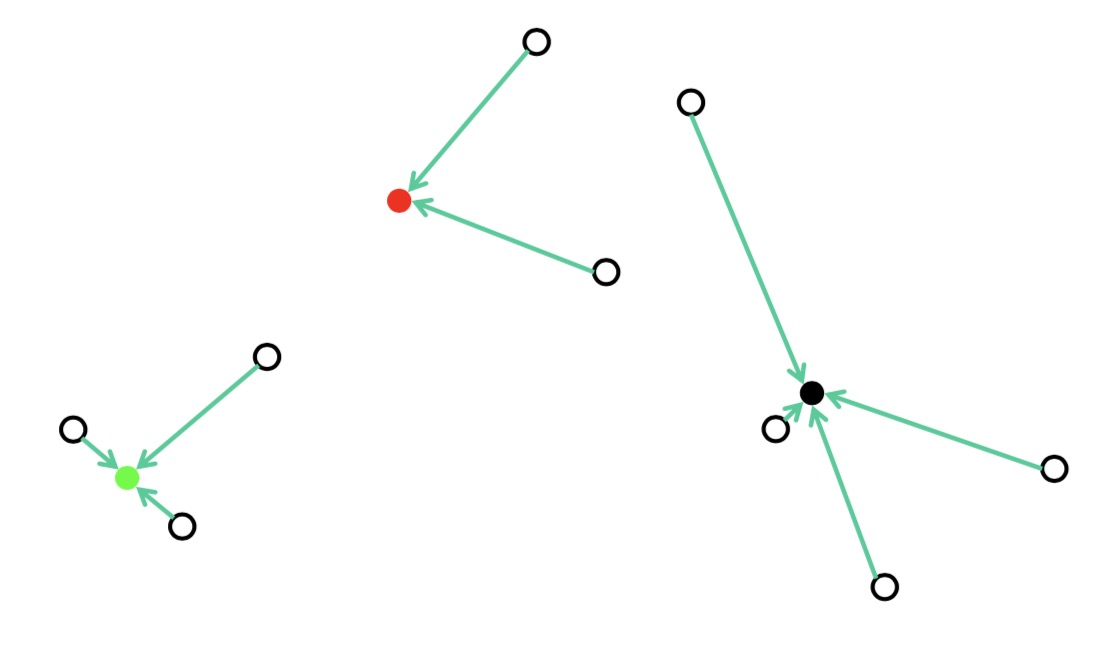
再次计算被分类点的均值作为新的中心点
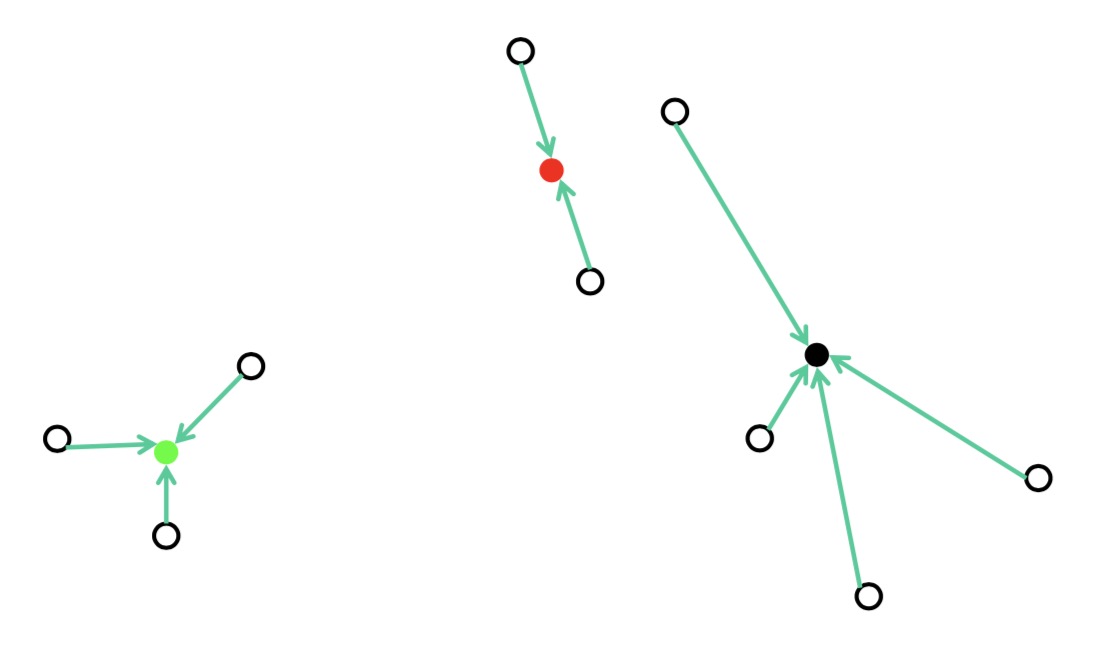
再次更新距离中心点最近的点
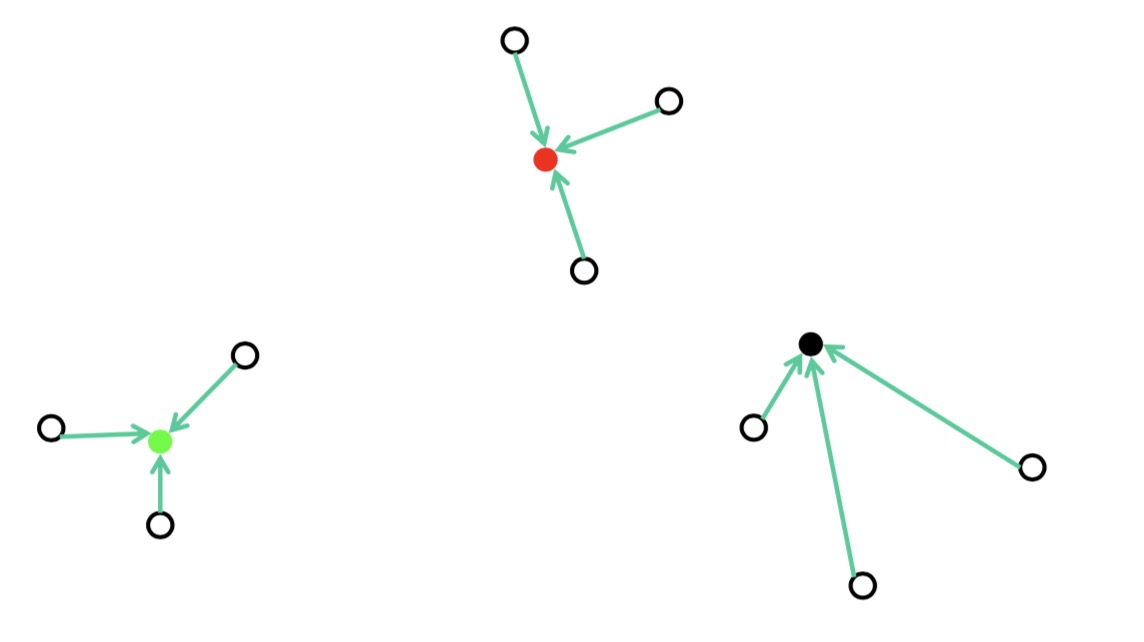
计算中心点
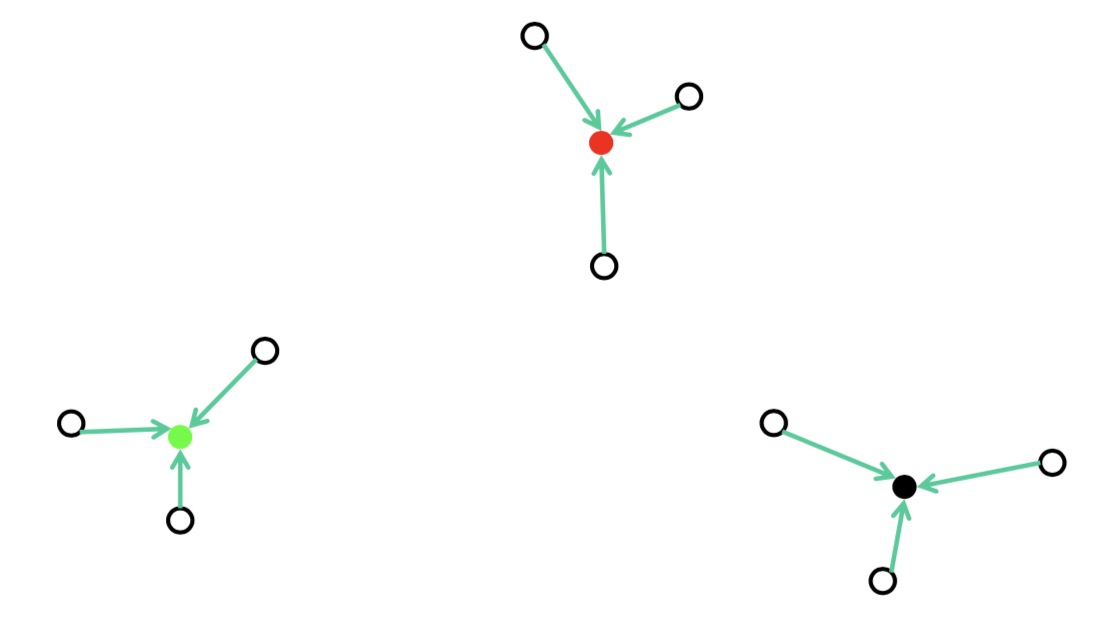
当所有的点无法再更新到其他分类时,算法结束,此时继续迭代,聚类中心将不会再做改变。
k-means算法,输入有两个部分:K(聚类的个数):number of clusters,训练集$x^{(1)},x^{(2)},…,x^{(m)}$
随机初始化K个聚类中心$\mu_1,\mu_2,…,\mu_k$,重复以下迭代:
for i=1:m
$c^{(i)}$=从1到K的所有聚类中心索引(index)中最接近于$x^{(i)}$的索引,即
for k=1:K
$\mu_k$=对于接近于聚类k点处平均值,即
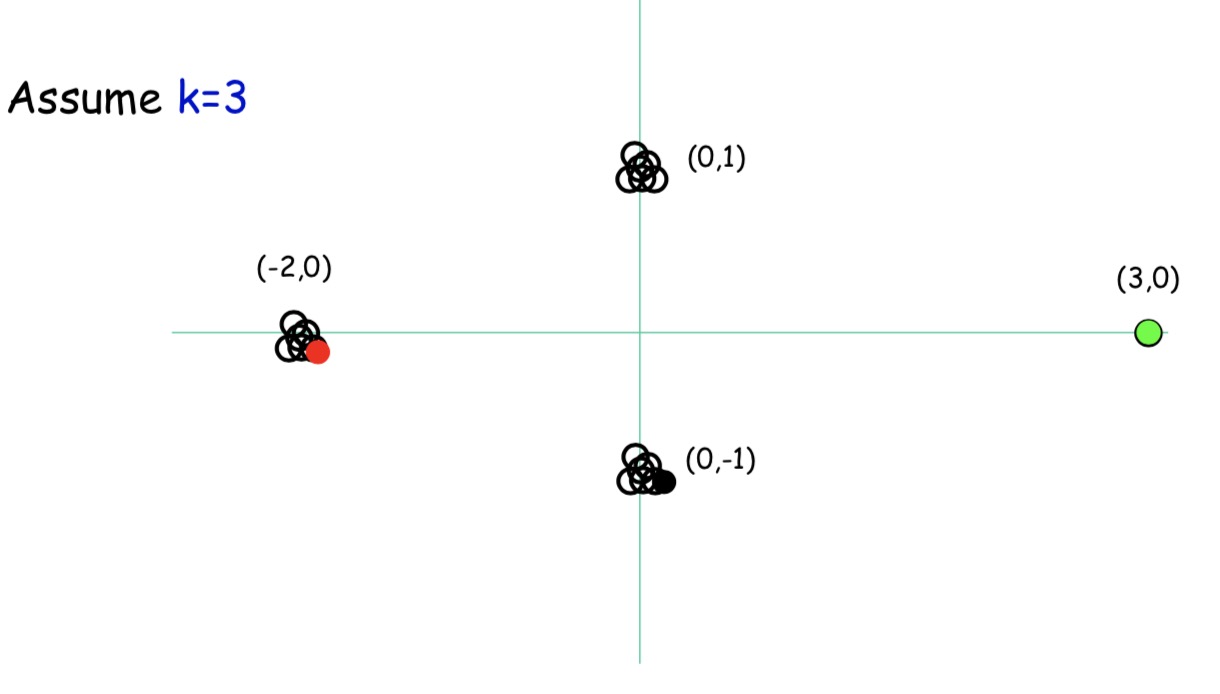
但是,k-means也有其缺点,例如,我们有9个点,初始点我们选择了图中的这三个
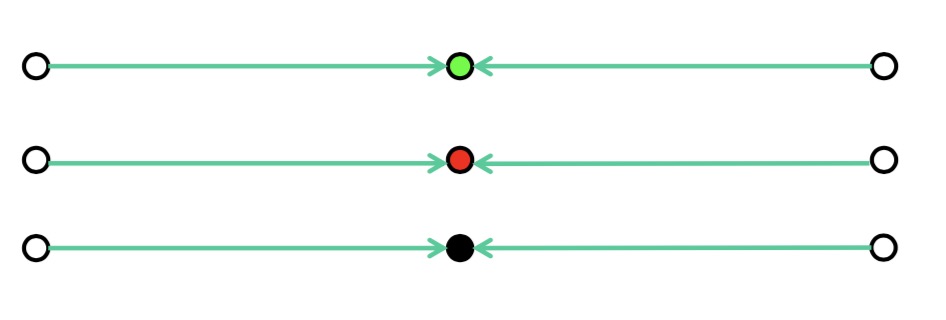
根据前面的算法,我们最终的结果是这样的
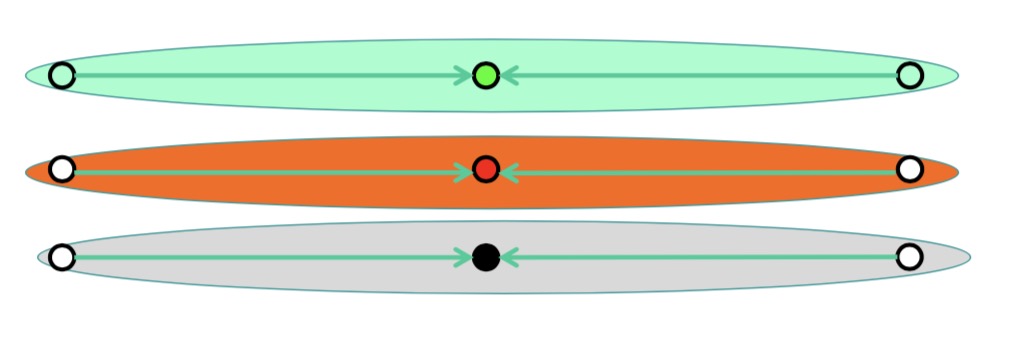
显然,这并不是我们期望的结果,算法最终陷入到了局部最优解中。
最远点初始化
从上面的问题就可以发现,其实k-means算法的关键就是找到合理的初始化点,初始化点的位置会影响到最终的结果好坏。这里我们介绍一种优化方案,最远初始化。
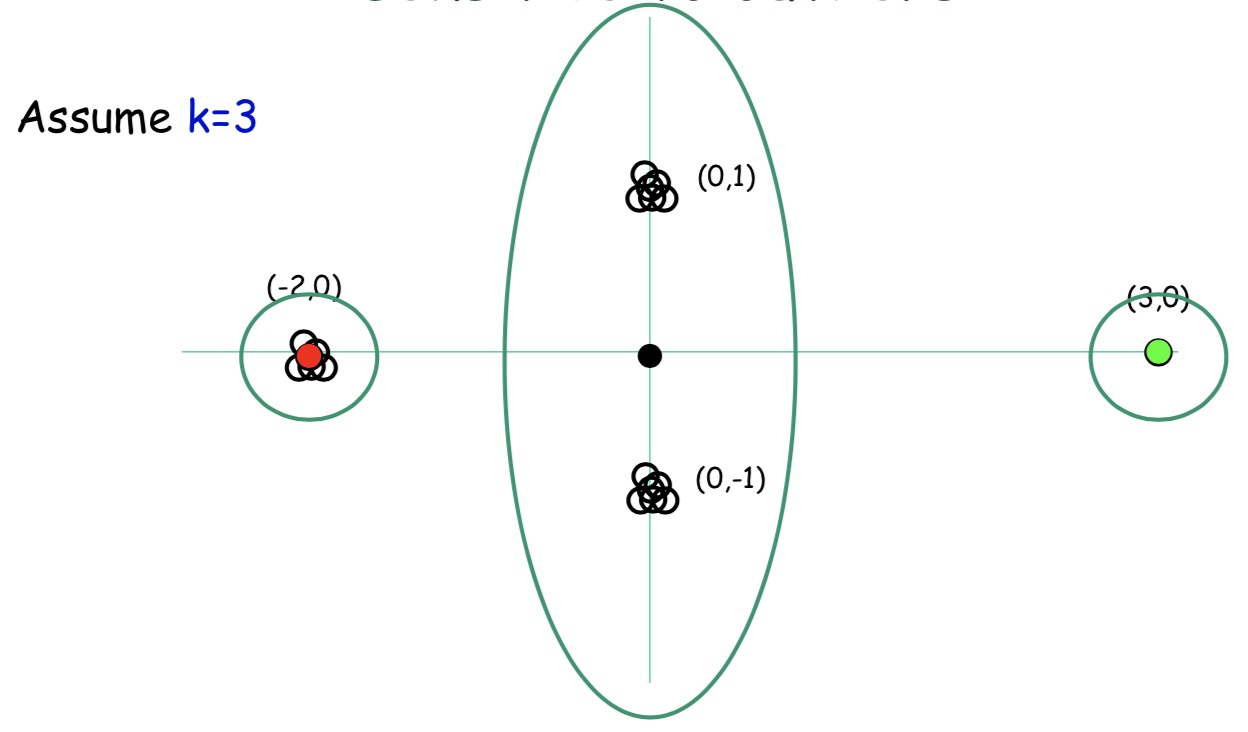
首先,我们还是随机选一个点,例如图中的红点
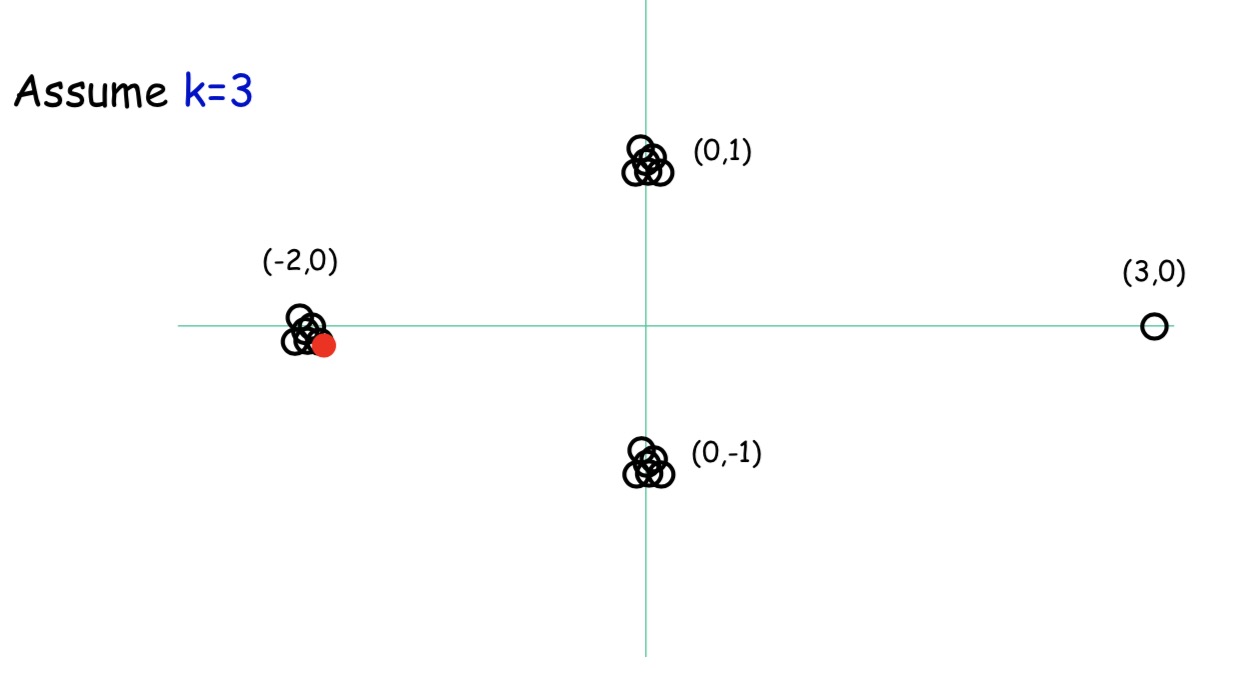
接下来,我们要选择一个距离红点最远的点,图中绿点
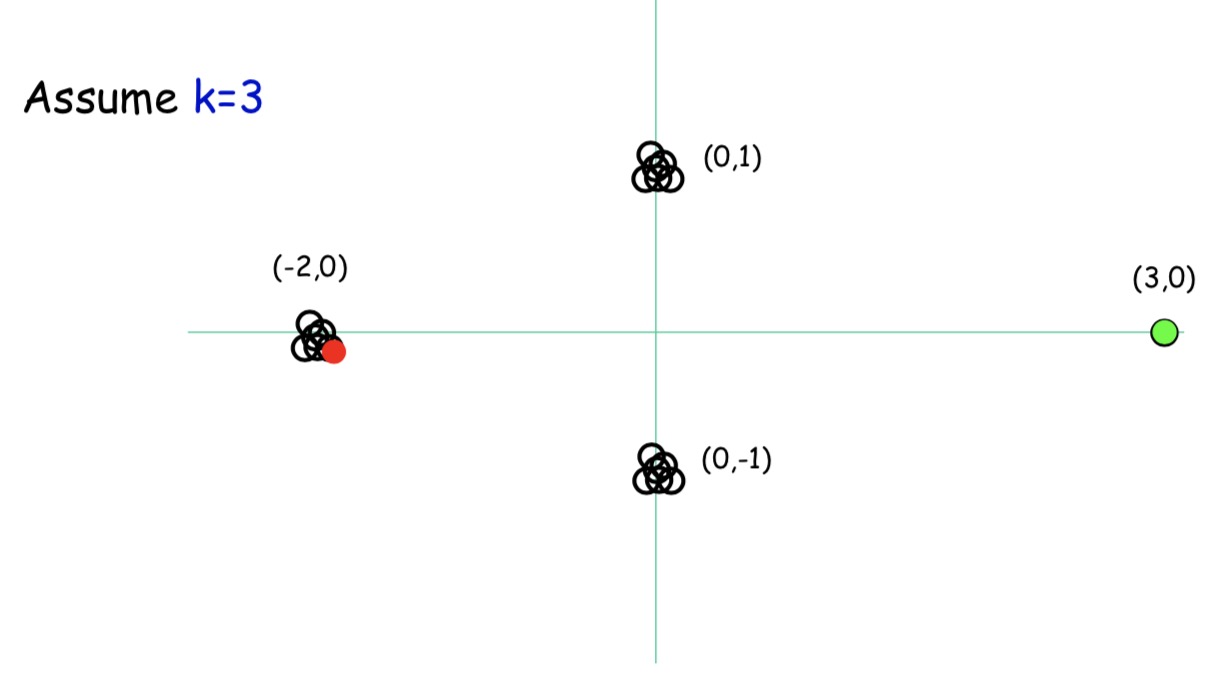
最后,再选一个距离红点第二远的点,图中黑点
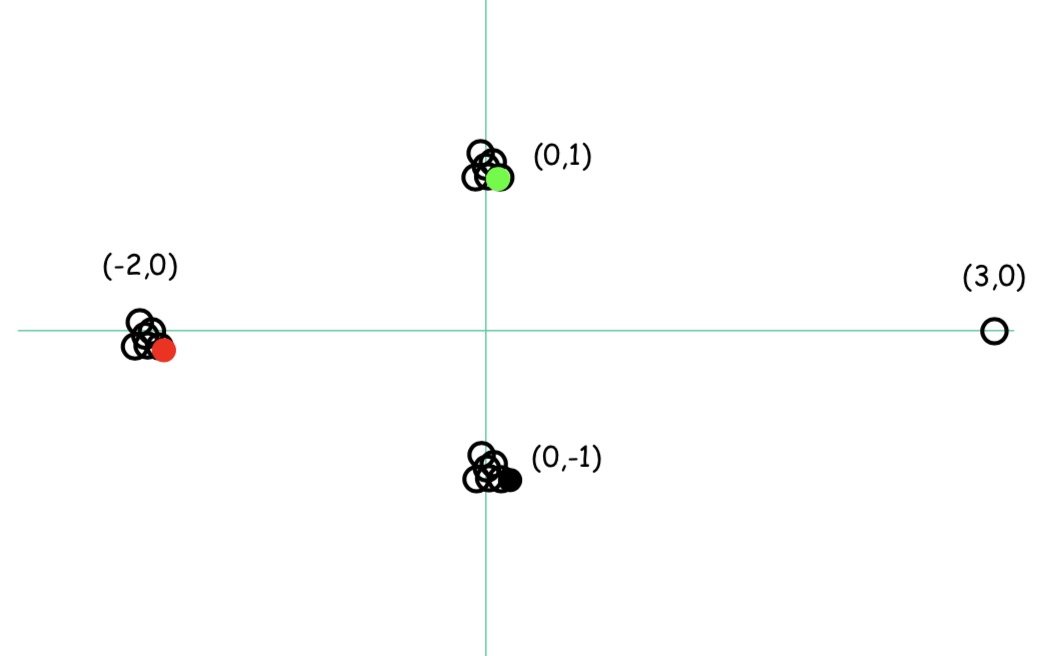
初始化完成后根据前面提到的算法完成分类
但是,该算法还是有一些问题,对于绿点,如果是噪声的话,我们最终把噪声分成了一类,这也并不是我们想要的结果,那么怎么解决这个问题呢?
K-means++
对于噪声,我们知道都是一些很少量的数据,那么,在我们选择点的时候,我门要给所有的点一个权重,例如上面的绿点,虽然距离最远,但是只有一个点,其权重较小,而对于(0,1)与(0,-1)附近的点很多,其权重就大。例如,我们设绿点的权重是1/10,(0,1)与(0,-1)的点权重是1/30,但是其数量很多,假设有10个点,那么权重就可以理解为多个点的和,那就是1/3,所以,最终初始化的点会选择(0,1)与(0,-1)附近,噪声问题也就解决了。
K-means算法首先需要选择k个点,每次要计算其余n各点的距离,假设每个点的维度是d,那么最终的时间复杂度是$O(nkd)$,可见其算法是线性的,效率很高。
K值的选择
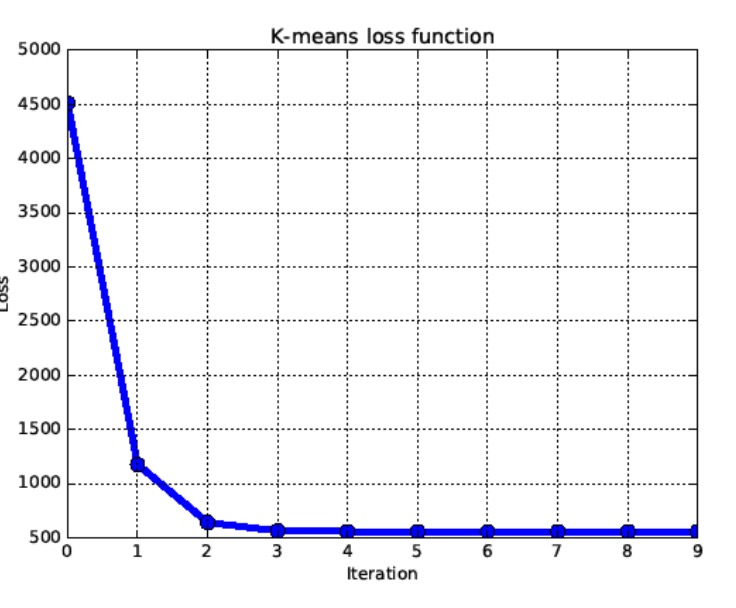
对于K值的选择,我们可以考虑使用交叉验证,根据损失函数来选择最优的K
损失函数最终会有一个拐点,根据这个拐点我们就能选择最佳的K值