树模型 - Welcome to AI World

前言

决策树（Decision Tree）是一种基本的分类与回归方法，该算法结构简明，计算成本低，方便做数据清理，相比神经网络的黑盒模型，其更有说服力，因此工业使用率是很高的。但是决策树也有其缺点，只能做线性分割数据，并且是一个贪婪算法。

决策树

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部节点和叶节点，内部节点表示一个特征或属性，叶节点表示一个类。分类的时候，从根节点开始，对实例的某一个特征进行测试，根据测试结果，将实例分配到其子结点；此时，每一个子结点对应着该特征的一个取值。如此递归向下移动，直至达到叶结点，最后将实例分配到叶结点的类中。

为了方便理解，我们来看例子

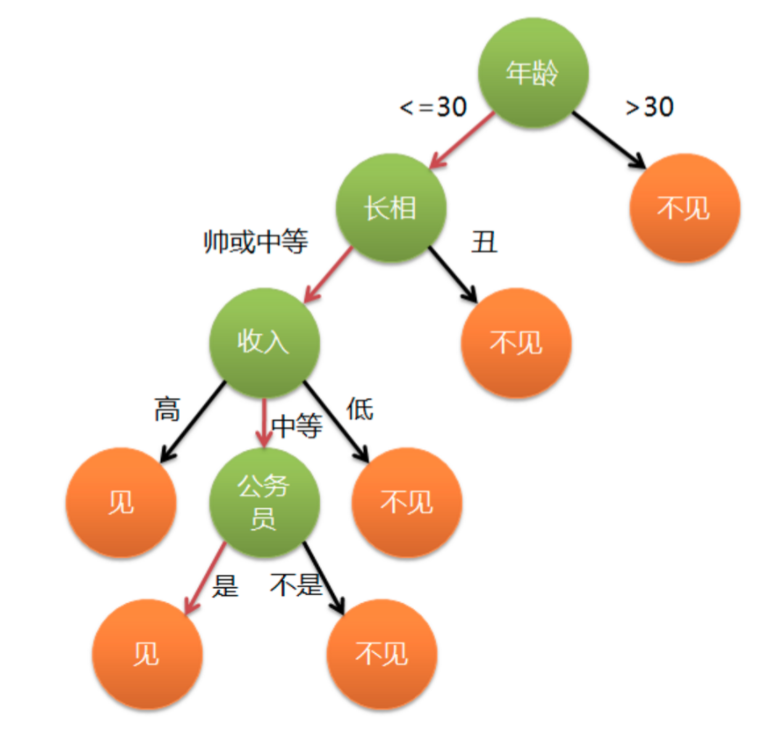
一个女孩子去相亲，其择偶的标准是年龄，长相，收入，是否是公务员。其中绿色结点表示判断条件，橙色结点表示叶节点即决策结果，箭头表示在一个判断条件在不同情况下的决策路径，图中红色箭头表示女孩的决策过程。当把一个人的条件输入到如图的树行结构中，最后就会输出一个是否见面的结果。这就是一个最基础的决策树模型。

决策树的关键是分治思想，能否把数据分成两组，不同的数据点能否被完美区分开(pure)

接下来我们再看一个带有数据的例子，这个是小明14天内是否去打球的数据，我们的任务是根据这14天的数据来判断第15天他是否会去打球。

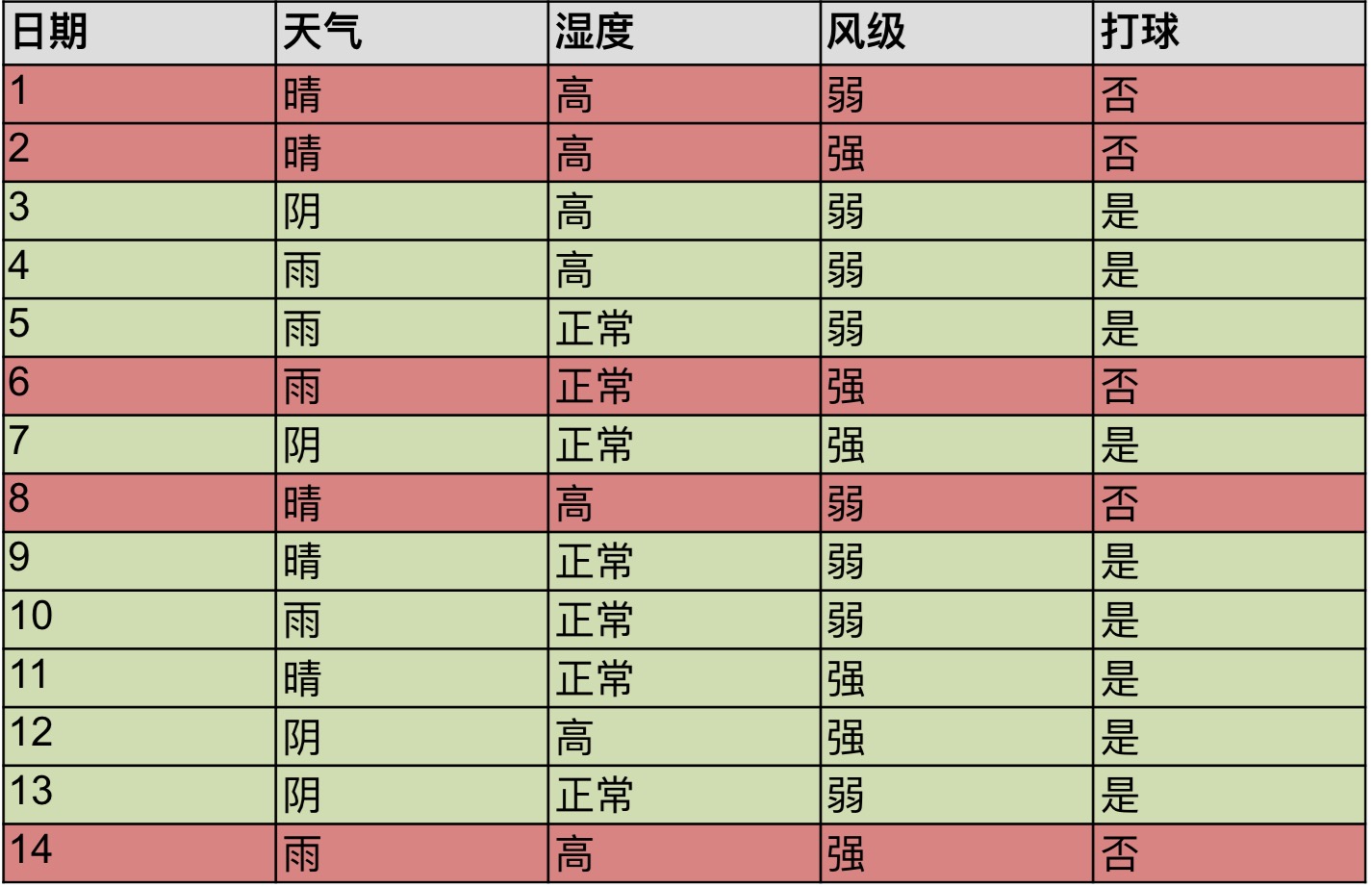
那么，小明是否打球是否是天气决定的呢

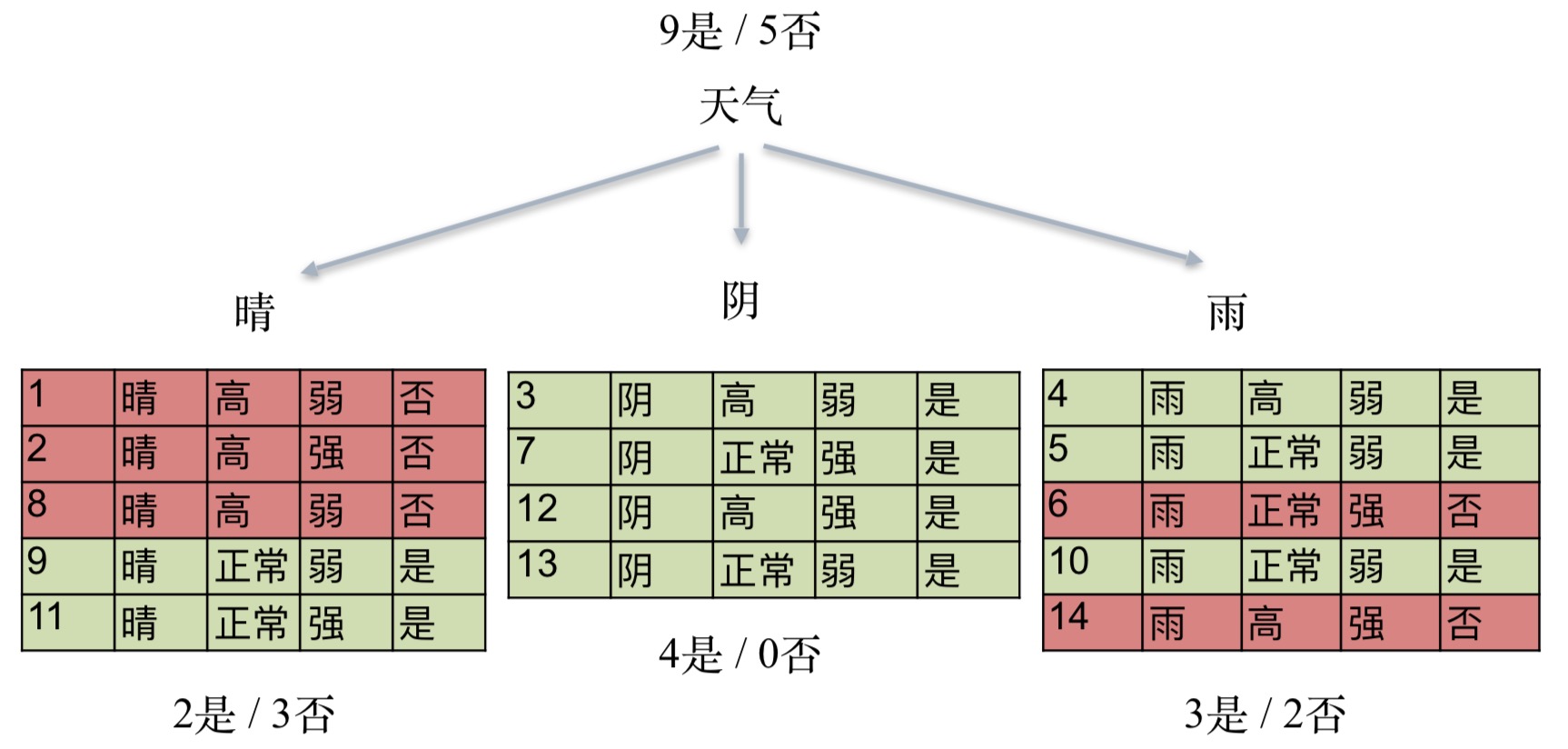
在天气的条件下，我们把它分为了3类，但是晴天与雨天并没有完美区分开是否打球，也就是说这个是不pure的，因此，我们需要对该类进行进一步的区分。

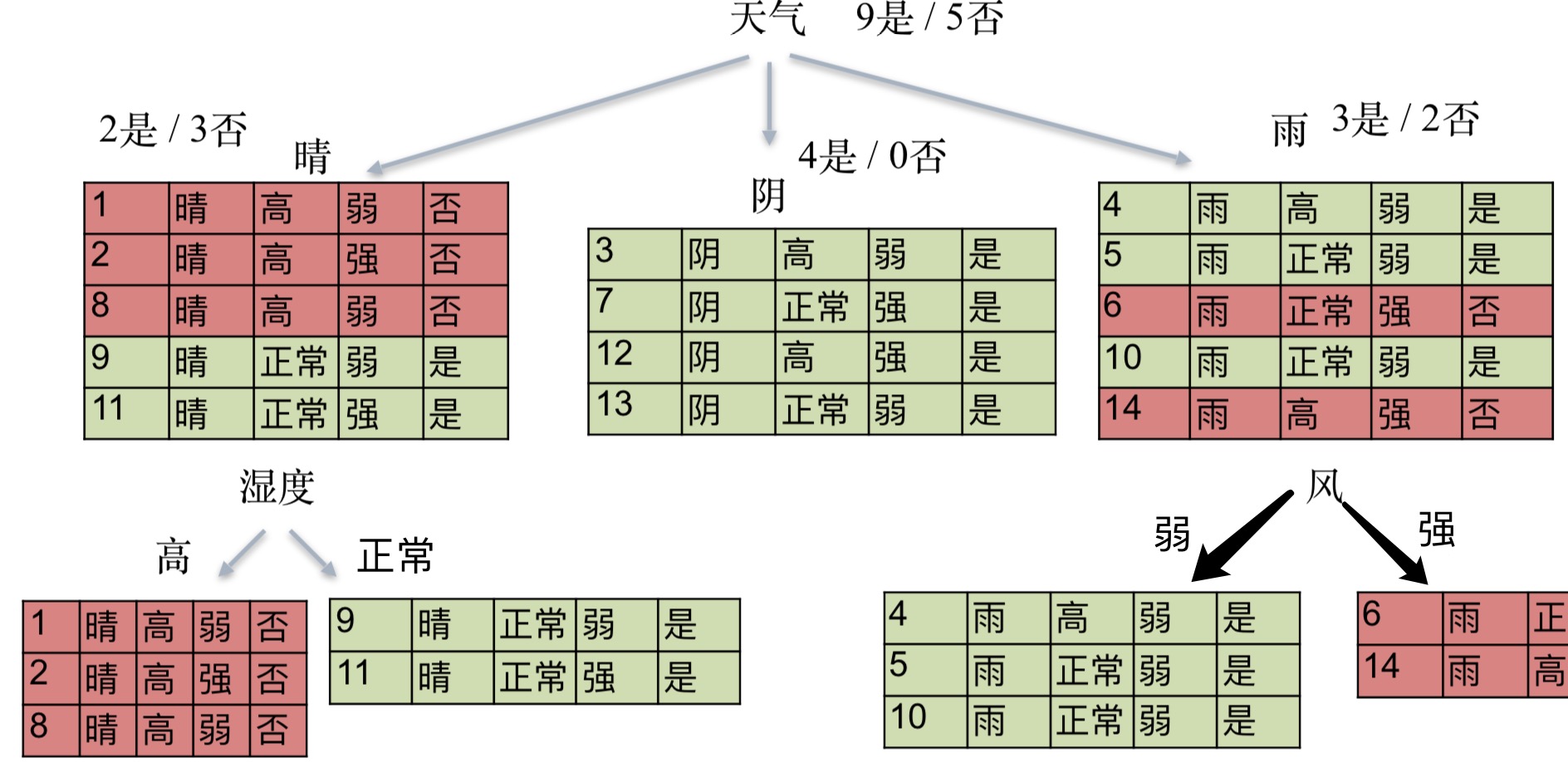
我们针对晴天用湿度这个特征进行进一步的分类，对雨天用风的强弱来进行进一步分类，最终完美区分开。到这一步，就是我们最终的决策树。

那么，在分类的是否，我们改选用什么特征作为第一个分类呢，是天气还是湿度？这就需要引入一个新的概念，熵Entropy

熵Entropy

熵是用来形容物体的一个混乱状态的，如果越混乱熵就越高。例如上面的是否打球，如果是与否各站一半，则熵较大，反之较小，从函数图中可以看到，当取0.5的时候熵最大，取0或1时熵最大。因此熵能计算出按照某个特征分类后纯洁度(pure)有多高。

熵Entropy公式如下，其中k指类别数

$H(S) = -\sum_{i=0}^kP(x)logP(x)$

例如有6个数据，3个是，3个否

$H(S) = -\frac{3}{6}log\frac{3}{6}-\frac{3}{6}log\frac{3}{6}=1$

例如6个数据，6个是，0个否

$H(S) = -\frac{6}{6}log\frac{6}{6}-\frac{0}{6}log\frac{0}{6}=0$

那么，选哪一个特征才能选到最大的熵值呢

信息增益Information Gain

信息增益是指未分类前的熵减去分类之后的熵的差值，这个值越大越好

$Gain(S,A) = H(S)-\sum_{v=0}^k H(S_v)$

例如，我们这里以风为第一个分类，最终结果是9个是，5个否，那么以风为特征的熵为

$H(S) = -\frac{9}{14}log\frac{9}{14}-\frac{5}{14}log\frac{5}{14}$

我们是以风的强弱做为分类，强风6个是2个否，弱风3个是2个否，熵分别为

$H(强风) = -\frac{6}{8}log\frac{6}{8}-\frac{2}{8}log\frac{2}{8}$ $H(弱风) = -\frac{3}{5}log\frac{3}{5}-\frac{2}{5}log\frac{2}{5}$

根据公式，最终的信息增益

$Gain(S,A) = H(S) - H(强风)- H(弱风)$

ID3

应用以上两个概念，我们就有现在ID3算法 1.对当前样本集合，计算所有属性的信息增益 2.选择信息增益最大的属性作为测试属性，把测试属性取值相同的样本划为同一个子样本集 3.若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处,否则对子样本集递归调用本算法

但是ID3也有其缺点，它可以把N个数据分成100%纯洁的N组，例如上面的例子，如果按照日期分成14个组，那么也是完成纯洁的，但是却导致了过拟合，且分组毫无意义。

那怎么避免过拟合呢，这里有两个方案

没必要的分类不要做

例如空气质量是否会影响小明去打球，如果影响率小于25%，那么这样的分类是没有意义的
减枝Prune

例如小明打球的14天数据，我们只用其中10条数据去测试，剩余4条数据作为验证集，当我们用10条数据生成一个树之后，将验证集的数据喂进去，并随机减去一个分类，如果最终仍可以将数据分类成功，那么这个枝就是多余的，是不要分这个类的。

信息增益比Gain Ratio

对于信息增益来说，也有其缺点，如果按照日期分成14个组，由于分类后的熵都为0，所以最终的信息增益

$Gain(S,A) = H(S)$

因此，我们这里又引入了一个新的概念，信息增益比

$GainRatio(S,A) = \frac{Gain(S,A)}{\sum_{v=0}^k H(S_v)}$

由于结果是一个比值，分母不能为0，从而解决了上面的14个分类的问题。C4.5算法就是在ID3算法的基础上引入了Gain Ratio。

决策树的优化

针对于决策树的缺点，在之后的研究中，又提出了一种森林的结构，即多棵树，这里为大家介绍三种森林的结果

Bagging

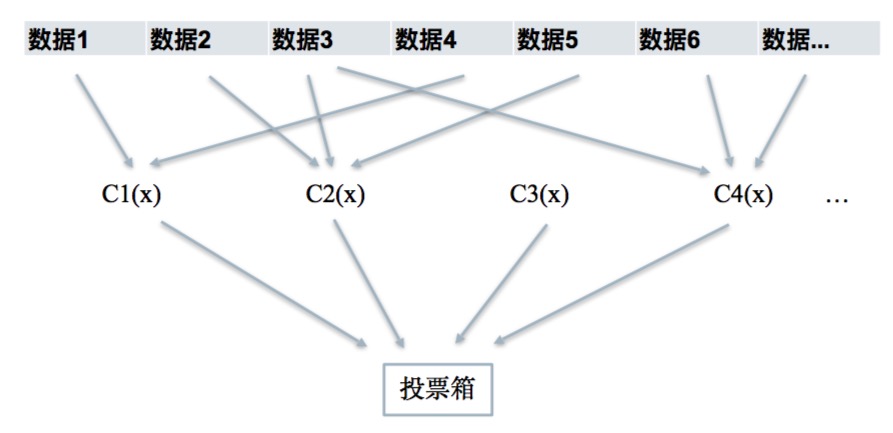
Bagging的结构如果，我们生成了C棵树，每棵树获取到的样本数据不是所有的特征，而是选取了一部分特征，例如某数据的A特征含有噪音，但是因为不同的树只选择了一部分特征，最后有的树是不会获取到含有噪音的特征的，最后再把所有的树的结果汇集起来，像投票一样，取得票率最高的作为最终结果

随机森林 Random Forest

随机森林在Bagging的基础上，添加了随机样本的选择，即不是每一棵树都能获得所有数据而是一部分数据。注意，随机森林不能做任何剪枝，最后结果依然做投票选择。

Boosting

$C(x) = sign[\sum a_mC_m(x)]$

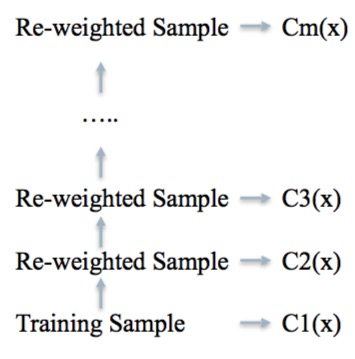
Boosting的原理和其它两个不太相同，而是先生成一课树，当分类结束后，找分类不好的数据，并给予一个相对较大的权重（这个权重怎么选择我们会在下文讲解），再用新的树进行训练，这时新树会针对权重较大的数据进行较好的分类，这样多次的循环，最终结果由加权投票决定。

AdaBoost

AdaBoost是一种Boosting结构的算法,我们会以AdaBoost讲解下权重怎么计算

1.初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权值:1/N 2.第一课树训练完后，比较训练结果与实际结果，并统计出误差率$e_m$，例如1000个数据，有100个数据分错，那么误差率$e_m = \frac{1}{10}$，并且将这个值作为数据集新的权重 3.计算树的权重$a_m$，树的权重是指这棵树被信任的程度有多高。$e_m <= 0.5$时，$a_m >= 0$，且$a_m$随着$e_m$的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

$a_m = \frac{1}{2} log \frac{1-e_m}{e_m}$

最终分类器为：

$G(x) = sign(\sum_{m=1}^M a_mG_m(x))$

GBDT

Gradient Boost Decision Tree是工业上做的较好的一个树结构，它是AdaBoost的一个regression版本，以下是具体的区别。

GBDT的误差计算并不是单纯的统计有多少数据错了，而是有一个特定的误差方程
新一课树的训练数据不是原始数据，而是原始数据的残差项，例如，我们在预测一个人的年龄，实际年龄是18岁，但是第一课树计算出的结果是12岁，相差了6岁，即残差是6岁，那么下一课树训练的时候就把改数据设为6去训练，如果最终训练结果是6就分到6岁的叶子节点，不过不是就继续计算残差使用下一课树训练。
最终结果是加权和值得到，不再是多数投票

XGBoost

本质还是个GBDT，但是是把速度和效率做到了极致，所以叫X (Extreme) GBoosted

在计算新的权重时，添加L1 L2 Regularization防止过拟合
对cost function一阶和二阶求导
树长全后从底部向上剪枝，防止贪婪算法

决策树与随机森林

前言

决策树