支持向量机SVM - Welcome to AI World

前言

SVM - support vector machine, 俗称支持向量机，为一种supervised learning算法，属于classification的范畴。本篇文章将会讲述SVM的原理并介绍推导过程。

如图，我们有些红色与蓝色点分部在平面中，我们设蓝点为正红点为负。SVM的任务就是找到一条线，将红点和蓝点分割开来，这条线可能会有很多种可能，图中绿色的实线是最好的一条，因为它距离红点和蓝点所在的虚线的距离最大。

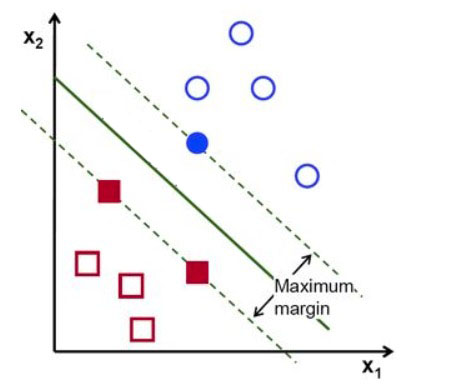
接下来我们就一起来探讨下SVM的这条分割线是如何找到的。

首先，我们先随便找一条线做为分割线，我们选择平面上的任意一个点用向量$\vec{u}$表示，设分割线的法向量为$\vec{w}$，就可以计算出向量$\vec{u}$ 在$\vec{w}$ 方向的投影长度。

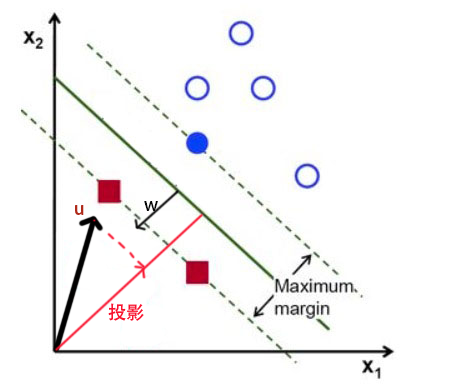
假设分割线距离原点的距离为b，那么对于负样本$\vec u$

$\vec{u} · \vec{w} <= b$

就有

$\vec{u} · \vec{w} - b <= 0$

从公式就能看到，SVM其实就是要寻找合适的$w$与$b$让虚线与实线的距离最大。

接下来我们把实线与虚线的距离归一化，那么对于训练集来说就有如下公式

负项：

$\vec{w}\vec{x} - b <= -1$

正项：

$\vec{w}\vec{x} - b >= 1$

为了将这两个公式统一，我们加入一个辅助量

$y_i = \begin{cases}\;\;1\quad x为正\\-1\quad x为负\end{cases}$

把辅助量带入上面的公式，最终两个公式可以合并成一个公式

$y_i(\vec{w}\vec{x} - b) - 1 >= 0$

那么，怎么样才能保证实线与虚线的距离最宽呢，这里我们设$\vec x_+$与$\vec x_+$分别为正负虚线上面的点，那么就有

$width = (\vec x_+ - \vec x_-)· \frac{\vec w}{|w|}$ $x_+=\frac{b+1}{\vec w}$ $x_-=\frac{b-1}{\vec w}$

最终我们得到公式

$width = \frac{2}{|\vec w|}$

所以宽度实际上和训练数据是没有关系的，只要知道了法向量，就可以求出宽度

我们要让宽度越大越好，即

$max\frac {2}{|\vec w|}$

即

$min|\vec w|$

即

$min\frac{1}{2}|\vec w|^2$

这里添加的参数是为了之后求导方便

接下来就是求极值，但是我们这里有一个限制条件，因此根据拉格朗日乘子法,最终求极值的公式为：

$L = \frac{1}{2}|\vec w|^2 - \sum_{i=1}^N \alpha_i[y_i(\vec w_i \vec x_i-b)-1]$

对$w$与$b$求偏导

$\frac{\alpha L}{\alpha \vec w} = \vec w - \sum_{i=1}^N\alpha_i y_i x_i$ $\frac{\alpha L}{\alpha \vec b} = \sum_{i=1}^N\alpha_i y_i$

令导数为0有

$\vec w = \sum_{i=1}^N\alpha_i y_i x_i$ $\sum_{i=1}^N\alpha_i y_i = 0$

把这两个式子带入到L中

$L = \sum_{i=1}^N\alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N\alpha_i \alpha_j y_i y_j x_i x_j$

走到这一步我们会发现$w$与$b$已经别其他变量所取代，最后我们要求的是$\alpha$的值，对于$\alpha$的值，一般会采用SMO KKT等算法来求取，这里不做详细说明。

那对于一些无法用线性函数来做分类时怎么办呢

首相，我们会把数据做一个非线性变化，把值变化到一个线性可分的空间上，这个函数我们称为核函数kernel，根据上面的L公式来说，我们并不需要知道每个点的数据怎么变的，只需要拿到核函数的结果，并把$x_ix_j$替换成核函数结果即可求出最后的值。