Momentum算法讲解
前言
动量梯度下降法是对梯度下降法的一种优化算法,该方法学习率可以选择更大的值,函数的收敛速度也更快。梯度下降法就像下面这张图,通过不断的跟新w与b,从而让函数移动到红点,但是要到达最优解,需要我们不断的迭代或者调整学习率来达到最后到达最优解的目的。但是调大学习率会导致每一次迭代的步长过大,也就是摆动过大,误差较大。调小学利率会让迭代次数增加。而增加迭代次数则明显的增加了训练时间。动量梯度下降法不但能使用较大的学习率,其迭代次数也较少。

指数加权平均数
在理解动量梯度下降法之前,我们首先要了解指数加权平均数,这是动量梯度下降法的核心。那么,什么是指数加权平均数呢,我们这里举例说明。
下面是一个同学的某一科的考试成绩: 平时测验 80, 期中 90, 期末 95 学校规定的科目成绩的计算方式是: 平时测验占 20%; 期中成绩占 30%; 期末成绩占 50%; 这里,每个成绩所占的比重叫做权数或权重。那么, 加权平均值 = 80 * 20% + 90 * 30% + 95 * 50% = 90.5 算数平均值 = (80 + 90 + 95)/3 = 88.3
我们再看一个例子,这是一个城市每天的温度
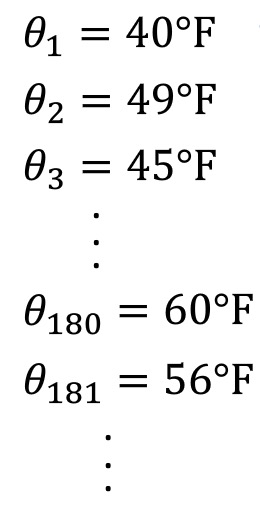
普通的温度平均值是
在计算加权平均数时,我们引入了一个变量$\beta$作为权重,就好比上一个例子的成绩占比,我们先看下公式
其中$v_t$代表前$t$天的平均温度,$\theta_{t}$代表第$t$天的温度,其中$v_0=0$。在坐标轴中绘出其形状,蓝点是每天的具体温度,红线是指数加权平均数。
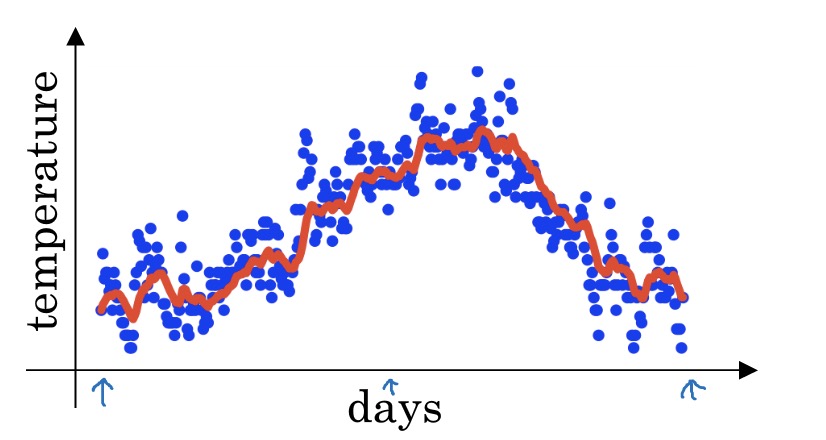
接下来我们详细讲解下这个公式,首相,我们把公式展开
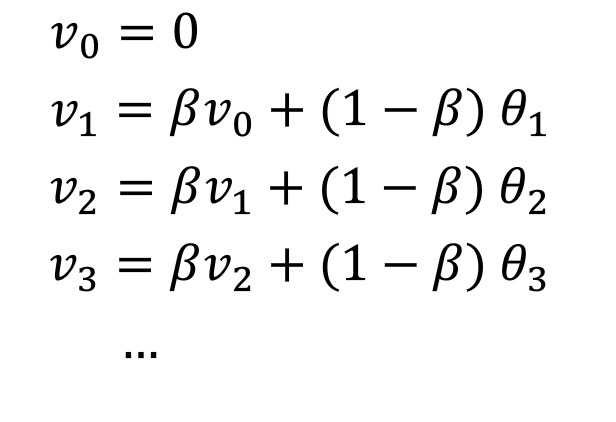
假设$\beta=0.9$,那么,我们得到的公式如下
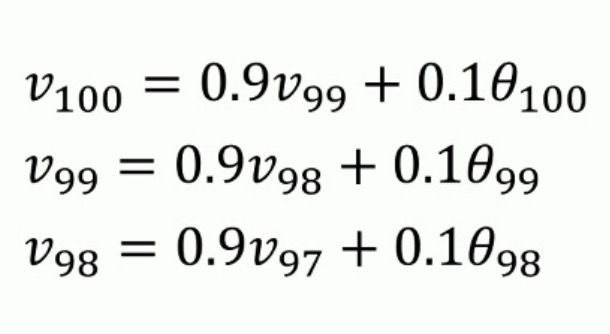
我们把$v_{99}$ $v_{98}$带入到$v_{100}$中
可以发现,其实我们最终是给每一个值都赋予了一个权重,这个权重距离$t$越近,权重越大,反之也越小。但是因为越是后面的值,权重越小,所以算出来的值是可以忽略的,所以选择$\beta$时是很关键的,这里有一个公式
这个公式得到的值即为迭代范围,例如$\beta=0.9$计算结果为10,那么,计算出来的加权平均数就是对过去10次进行迭代。
那么,我们为什么要使用加权平均数呢,其实,在训练过程中,数据量是很大的,假设训练样本有100w,即使mini_batch取100,其计算平均值消耗的内存和时间需要的代价都很大,而对于加权平均数,如果$\beta$取值0.9那么只需要计算10个数即可计算其平均值,大大节约了内存,计算效率也极大的提高了。
动量梯度下降法
我们先回顾下普通的梯度下降法在更新参数时
而对于动量梯度下降,首先,我们针对$dW$计算出$v_{dW}$
在更新参数时,我们不是乘$dW$,而是
这里我们又引入了一个超参数$\beta$,经过实践,这个超参数建议取0.9效果较好,大家也可以根据实际情况进行调整。
那么,为什么乘加权平均数就可以加快收敛的速度呢,我们再看下这张图

正常情况下(图中蓝色线段),函数会在纵轴上不停的波动,但实际上纵轴上的这些波动的平均值是接近于0的,我们更希望其波动较小,在横轴上能快速前进。动量梯度就是通过计算其加权平均值,把这些在纵轴上多余的波动去除,从而让函数尽可能快的朝着横轴移动,因此其收敛的速度也会很快。



