Adam优化算法 - Welcome to AI World

前言

Adam 优化算法是随机梯度下降算法的优化，近来其广泛用于深度学习应用中，尤其是计算机视觉和自然语言处理等任务，该算法是Momentum算法与RMSprop算法的结合。动量梯度下降法Momentum我们之前已经讲解过，本文将会先介绍下RMSprop算法，再讲解Adam。

RMSprop(均方根)

在图中这样的情况时，梯度下降在横轴方向前进，在纵轴方向却会有大幅度的抖动。我们把横轴代表参数$w1$，把纵轴代表参数$w2$。注意，作为例子我们此处只引入了2个参数，实际情况会复杂很多。这里我们依然会使用指数加权平均数，如果你不了解指数加权平均数，请先阅览动量梯度下降法Momentum。 $S_{dw1} = \beta S_{dw1} + (1-\beta)(dW_1)^2$ $S_{dw2} = \beta S_{dw2} + (1-\beta)(dW_2)^2$

这里我们最后乘的是$(dW)^2$而不是$dW$，我的理解是$dW$的值可能会出现负数，而我们更新参数时，必须保证$S_{dw1}$为正数。

计算出指数加权平均数之后，我们开始更新参数

$W_1 = W_1 - \alpha \frac{dW_1}{ \sqrt[]{S_{dw1}+\epsilon}}$ $W_2 = W_2 - \alpha \frac{dW_2}{ \sqrt[]{S_{dw2}+\epsilon}}$

此处的$\epsilon$是为了防止分母为0

横轴$w1$因为抖动小，所以$dW_1$的值很小，$S_{dw1}$的值很小，最终与$\alpha$相乘的值就会很大，$W1$抖动变动大，在横轴就会前进的更快。

纵轴$w2$因为抖动大，所以$dW_2$的值很大，$S_{dw1}$的值很大，最终与$\alpha$相乘的值就会很小，$w2$抖动变小，纵向的变化相对平缓。

##Adam算法当把Momentum与RMSprop算法结合在一起时，就是Adam算法。

首先还是计算指数加权平均数，我们令$V_{dW}=0$、$V_{db}=0$、$S_{dW}=0$、$S_{db}=0$

接下来计算Momentum的指数加权平均数，注意超参数这里是$\beta_1$

$V_{dW} = \beta_1 V_{dW} + (1-\beta_1)dW$ $V_{db} = \beta_1 V_{db} + (1-\beta_1)db$

再计算RMSprop的指数加权平均数，注意超参数这里是$\beta_2$

$S_{dw} = \beta_2 S_{dw} + (1-\beta_2)(dW)^2$ $S_{db} = \beta_2 S_{db} + (1-\beta_2)(db)^2$

接下来进行参数修正，参数修正可以防止在迭代次数较少的时候，计算出来的指数加权平均数较小

$V_{dw}^{correct} = \frac{V_{dw}}{1- \beta_1^t}$ $V_{db}^{correct} = \frac{V_{db}}{1- \beta_1^t}$ $S_{dw}^{correct} = \frac{S_{dw}}{1- \beta_2^t}$ $S_{dw}^{correct} = \frac{S_{dw}}{1- \beta_2^t}$

最后更新参数

$W = W - \alpha \frac{V_{dw}^{correct}}{\sqrt[]{S_{dw}^{correct}+\epsilon}}$ $b = b - \alpha \frac{V_{db}^{correct}}{\sqrt[]{S_{db}^{correct}+\epsilon}}$

$\beta_1$常用的缺省值是0.9
$\beta_2$ Adam的发明者推荐使用的数值是0.999
$\epsilon$的取值没有那么重要,Adam论文的作者建议为$\epsilon=10^{−8}$
在实际使用中,$\beta_1,\beta_2,\epsilon$都是使用的推荐的缺省值,需要调整的是学习率$\alpha$

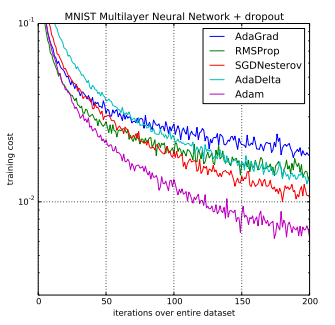
这是Adam 优化算法和其他优化算法在多层感知机模型中的对比，可见其收敛的速度较快，效果明显，并且Adam 算法很容易实现，有很高的计算效率和较低的内存需求。

Adam算法讲解

前言

RMSprop(均方根)